Une fois les surfaces développables bien modélisées, on a réalisé une définition grasshopper permettant de tracer les motifs de découpe de manière paramétrique, de manière à optimiser la densité du motif en fonction de la courbure de la surface. La définition Grasshopper suit les étapes suivantes.
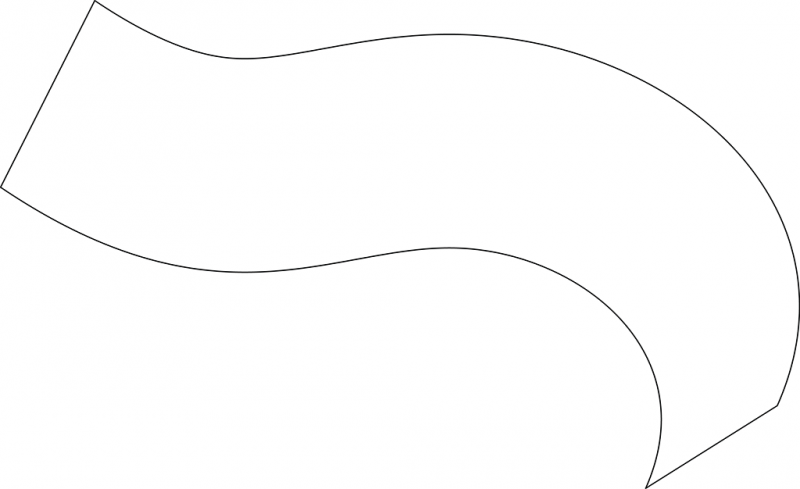
1.Récupération des courbures maximales le long de la surface
La courbure d’une surface en un point correspond à l’inverse du rayon de courbure du cercle osculateurs. On divise la surface en une grille plus ou moins dense puis on évalue sur chaque colonne quel est le cercle avec la plus grande courbure.
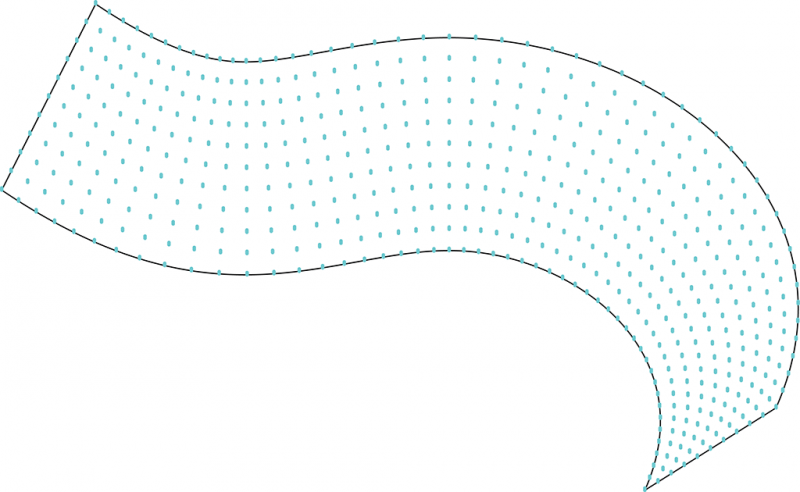
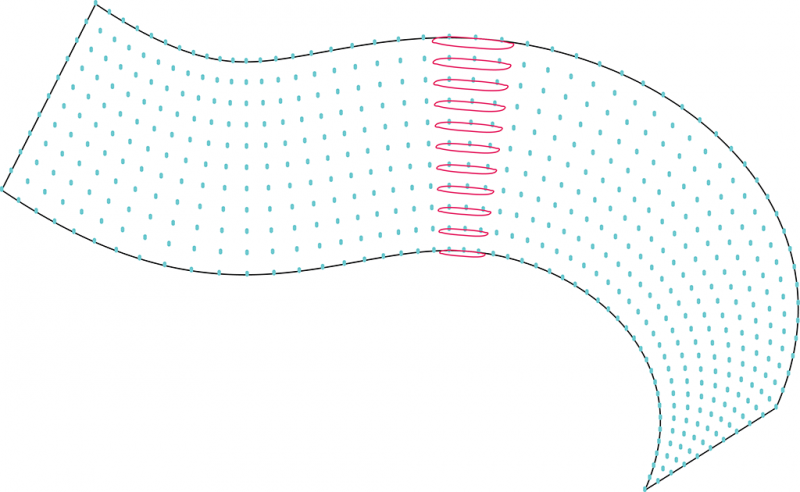
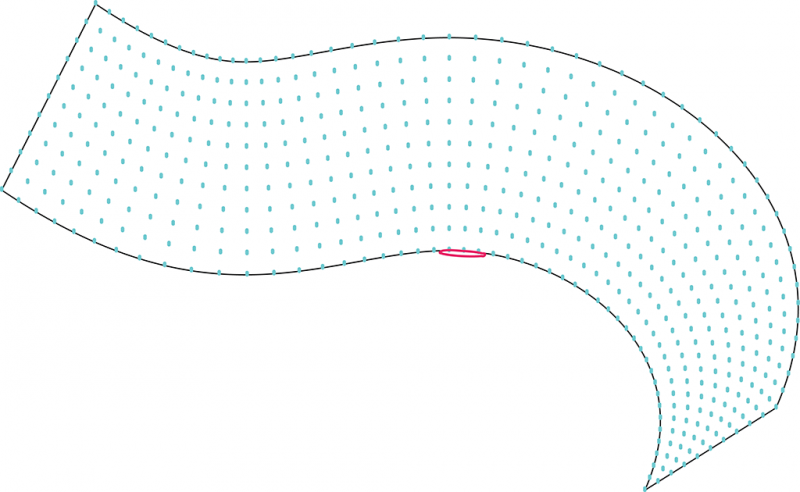
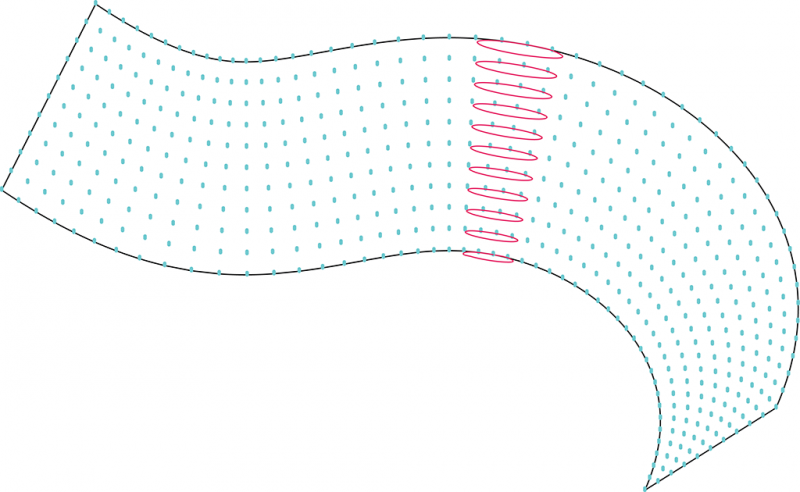
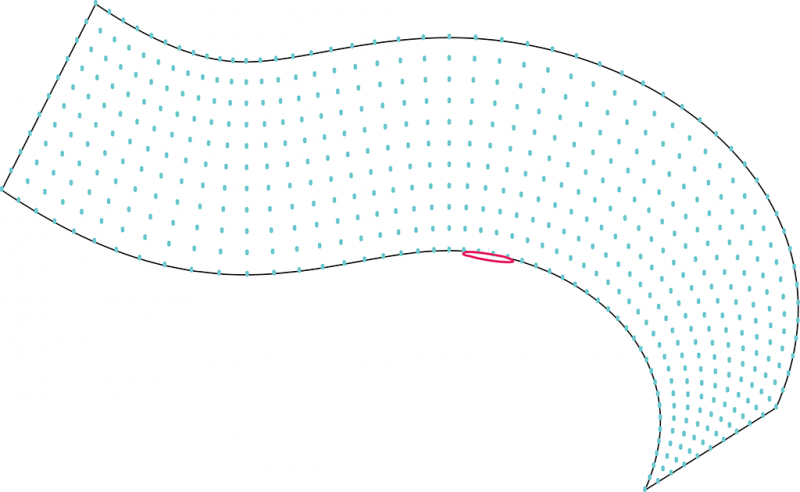
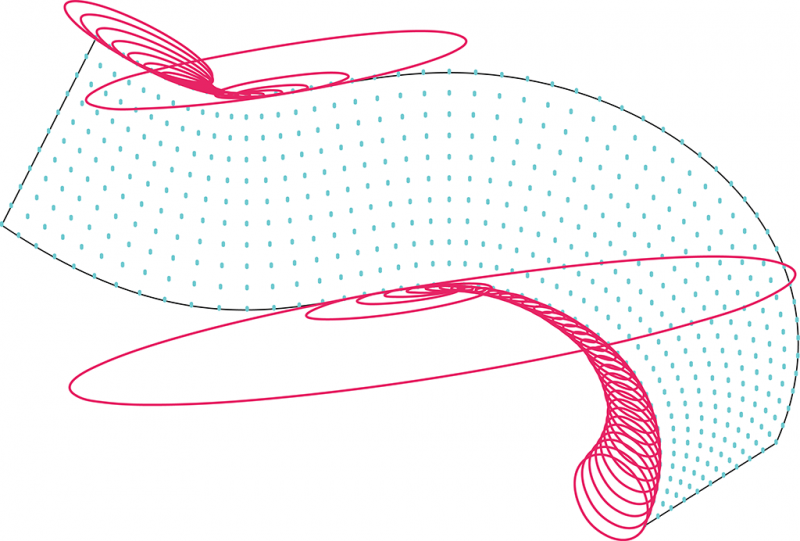
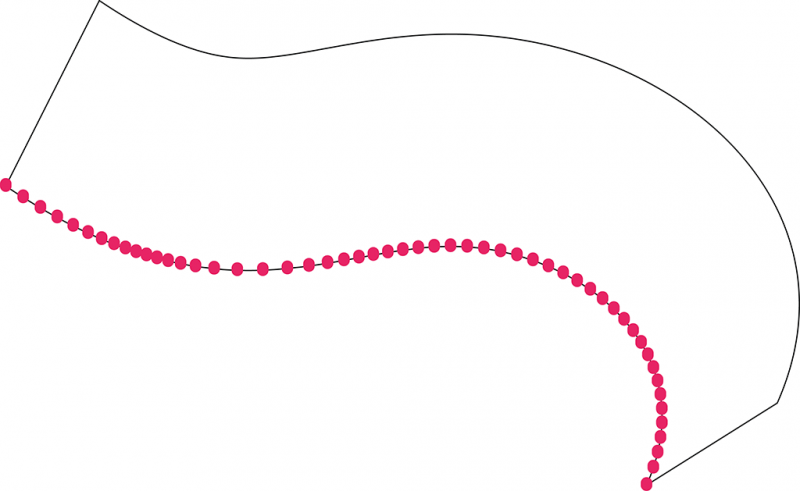
2. On a alors une série de courbure le long de la directrice. Un algorithme permet ensuite de répartir sur la directrice des points, avec une densité variable selon la courbure de la surface. On peut alors assez simplement découper la courbe en plusieurs portions, dont on évalue la courbure minimale pour la portion de surface correspondante.
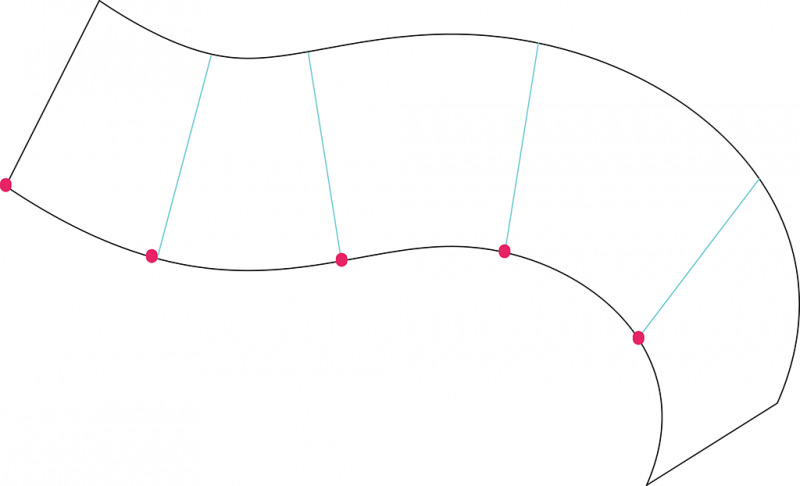
Ces portions ont chacune une valeur de courbure différentes qui va permettre de définir un n (nombre de jambes de torsion) ajusté selon la courbure de ces portions, ainsi que d’autres dimensions du motif.
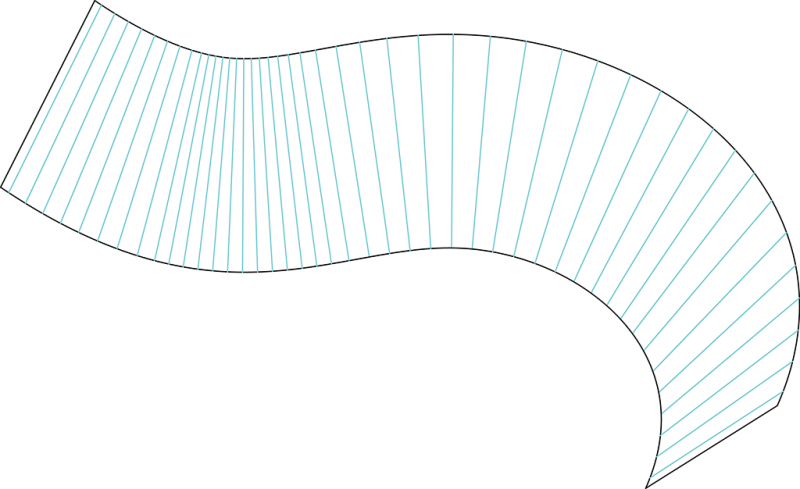
3.On récupère ensuite des séries de n génératrices par portion.
La surface avec les génératrice est déroulée sur un plan.
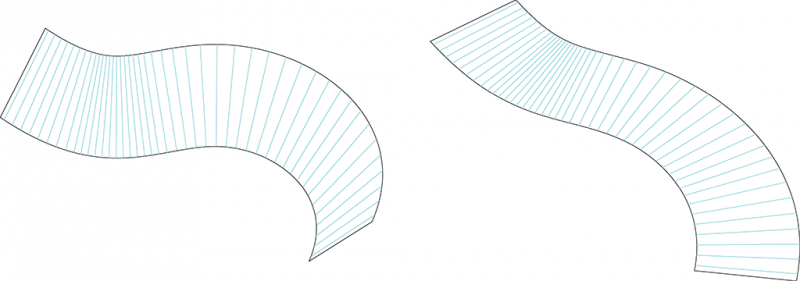
4.Puis par diverses opérations de liste, on trace le motif des jambes de torsion.
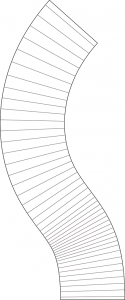
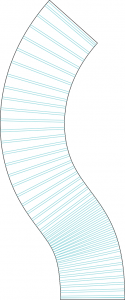
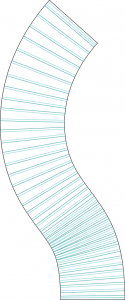
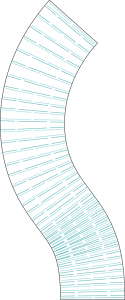
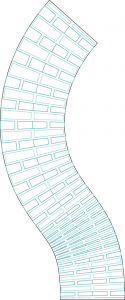
L’option open/close permet d’enlever ou non les parties de « trous » qui ne sont pas utiles à la torsion. Un filtre permet de répartir les motifs selon leur taille, pour éviter des surperpositions de découpe.
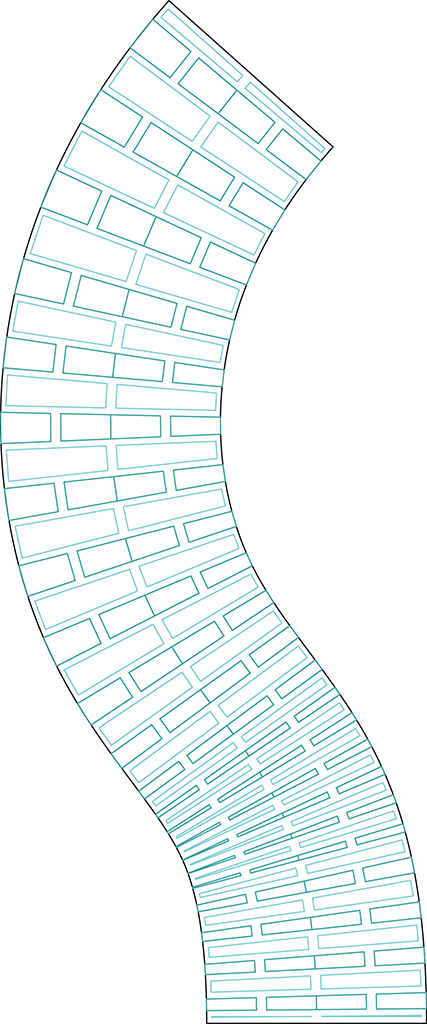
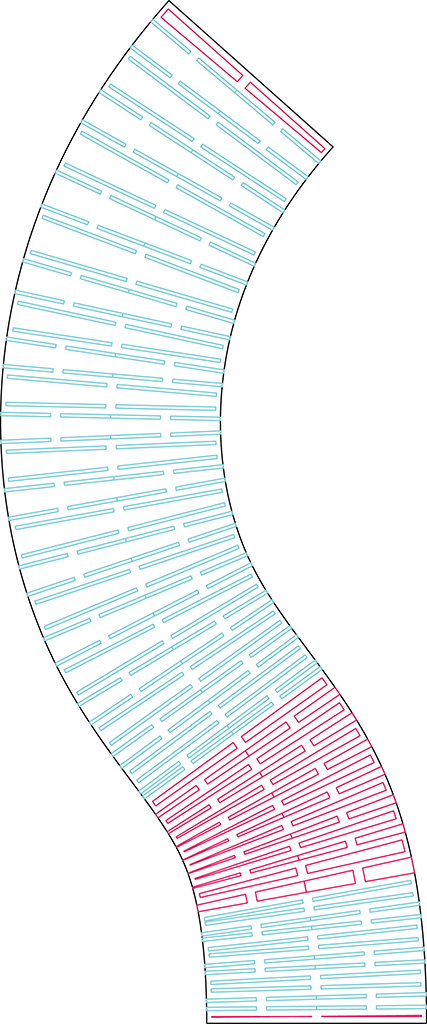
Pour une approche détaillée, voir le fichier grasshopper qui est à télécharger ici.
